Arşimet, klasik dönemin tartışmasız en büyük bilim insanlarından birisiydi. Bir matematikçi, fizikçi, astronom, mühendis, mucit ve silah tasarımcısıydı. Yazının devamında da göreceğimiz üzere, yaptığı çalışmalarla zamanının ötesinde bir insan olduğunu kanıtlamıştır.
Arşimet, Milattan önce 287 yılında Sicilya Adası’nda kurulan Yunan şehir devleti Siraküza’da dünyaya gelmiştir.
Hayatının İlk Yılları ve O Dönemde Antik Yunan
Antik Yunanların gerçek anlamıyla bilim yapan, bilim ile sadece merak ve öğrenme uğruna uğraşan ilk toplum olduğunu söyleyebiliriz. Her ne kadar diğer kültürler de bilimsel keşifler yaptıysa da bunlar sadece pratik fayda gözetilerek yapılmıştır. Güçlü tapınaklar nasıl inşa edilir ya da gezegen konumları tarım yapmak için ne zaman uygun olur gibi sorular hep pratik amaçlar içeriyordu.
Yunanlar ise sadece bilgilerine bilgi katmak amacıyla evreni araştırıyorlardı. Geometriyi, onun mantığı ve güzelliği için çalışırlardı. Hiçbir pratik amaç gözetmeksizin Demokritus, bütün maddelerin atom denilen küçük parçacıklardan oluştuğunu öne sürmüştü.
Bu atomlar daha küçük parçacıklara bölünemiyordu ve birbirleriyle çarpışarak sürekli hareket halindeydi. Demokritus bu anlayışı için mantıksal argümanlar üretmişti.
İşte Arşimet böyle bir Yunan kültürünün içine doğdu. Ünlü eseri The Sand Reckoner(Kum Sayacı) eserinde, babasının bir astronom olduğundan bahsediyor.
Arşimet, ömrünün çoğunu Siraküza’da geçirmiştir. Genç yaşında, Mısır’ın İskenderiye şehrinde yaşamıştır. İskenderiye şehri, Büyük İskender’in varisi Ptolemy Lagides’in inşa ettirdiği, o zamanlar dünyanın en büyük kütüphanesine ev sahipliği yapıyordu.
Arşimet’in çalışmalarının bazısı, Eratosthenes‘e gönderdiği mektupların kopyalarında muhafaza edilmiştir. Eratosthenes ise o zaman İskenderiye Kütüphanesi’nin müdürüydü. Dünya’nın çevresini gerçeğe yakın bir değerde hesaplayan ilk bilim insanlarından birisiydi aynı zamanda.

Arşimet’in Bilim Dünyası’na Katkıları:
Arşimet’ten 2000 yıl sonra, Rönesans zamanında matematikçiler, Arşimet’in çalışmalarına tekrar bakmıştır. Zaten Arşimet’in bulduğu sonuçların doğru olduğunu biliyorlardı fakat bu sonuçlara nasıl ulaştığı onlar için bir muammaydı. Örneğin bilimsel devrimin öncülerinden Galileo Galilei‘nin de Arşimet’in matematiği fiziğe uygulayışından çok etkilendiğini söyleyebiliriz.
Profesör Johan Heiberg, İstanbul’da 1906 yılında bir kitap keşfedene kadar ünlü matematikçinin gizemi çözülmemişti. Kitap 13.yüzyılda yazılmış Hristiyanlıkla ilgili bir dua kitabıydı. Bulunan bu kitabın ismi günümüzde Arşimet Parşömeni olarak biliniyor.
Heiberg, kitabın içindeki duaların, matematik işlemleri üzerine karalanmış olduğunu keşfetmişti. Duaları yazan bu keşiş, orijinal matematik çalışmalarını silmeyi denemiş. Geriye ise bu işlemlerin sadece izi kalmıştı.
Böylece bu matematik işlemlerinin aslında Arşimet’in çalışmasının kopyaları olduğu ortaya çıkmıştı. Ne büyük bir keşif ama! Arşimet yazıtları 10.yüzyılda kopyalanmıştı.

Kitap, The Method(Yöntem) dahil yedi bölümden oluşuyordu. Yöntem isimli bölüm ise yüzyıllar boyunca kayıptı. Arşimet, matematiği nasıl uyguladığını göstermek için Yöntem’i yazmıştı. İskenderiye Kütüphanesi’nde bulunması için onu Eratosthenes’e göndermiştir. Arşimet şöyle yazar:
Sanıyorum ki henüz keşfedemediğimiz teoremleri bulmak üzere bu kitabı kullanabilen gelecek nesiller olacaktır.
Yirminci yüzyıl matematikçileri, “Yöntem” eserini okuyarak Arşimet’in problemleri çözmek üzere kullandığı teknikleri ve zamanının ne kadar ilerisinde birisi olduğunu böylece öğrenmiş oldular. Bu keşif ve yöntemlerden bazılarını; Kaldıraç Kanunu, kütleçekim merkezini bulma yöntemi gibi keşiflerini fizikte kullanmıştı. Amacı ise matematikte yeni teoremler keşfetmekti.
Altın Taç Hikayesi
Pisagor gibi antik dönemlerde üstün yeteneklere sahip olan birçok önemli figür gibi Arşimet’in hayat hikayesi de yüzyıllar boyunca sayısız mitle ve efsane ile doldurulmuştur. Bunun sebebi de böyle özel insanların önemini vurgulamak ve efsaneleştirmektir. Arşimet hakkında bilinen en ünlü detaylardan biri de Siraküza sokaklarında “Eureka!, Eureka!” diye bağırdığı ünlü hikayesidir. Olay şöyle gelişir:
Kral II.Hiero, kendisine bir taç yaptırmak üzere bir ustaya belirli miktarda altın verir. Usta sonra tacı yapmış bir şekilde kralın yanına döner. Kral, tacı alır ve verdiği altınların ağırlığıyla tacın aynı olduğunu fark eder.
Fakat kral buna rağmen şüphelidir. Ustanın altınların bir kısmını kendisine ayırdığını ve yerine gümüş ekleyerek taç yaptığını düşünür. Bunun üzerine emin olamayan kral durumu Arşimet’e anlatır.
Arşimet Prensibi : Suyun Kaldırma Kuvveti
Bu konu üzerine haftalarca kafa yoran Arşimet. günün birinde bir şey fark eder. Banyo yaptığı sırada, suyun içinde alçaldıkça su taşıyor; suyun dibine çöktükçe vücudu daha az ağır geliyordu. Ya da kendini daha hafif hissediyordu. Bu aydınlanma anı üzerine Arşimet’in, Siraküza sokaklarına doğru koşup, “Eureka!”(Buldum!) şeklinde bağırdığı söylenir.
Arşimet Prensibi ya da Suyun Kaldırma Kuvveti olarak bilinen bu ilke, bir sıvıya kısmen ya da tamamen batırılan her cismin, taşırdığı sıvının ağırlığına eşit bir yukarı doğru kuvvet hissedecektir. Bu ilke, kralın tacı sorununda Arşimet’e yol gösterecekti.
Arşimet altının gümüşten daha yoğun olduğunu biliyordu. Böylece bir santimetre küp altın, bir santimetre küp gümüşten daha ağır gelecekti. Fakat tacın düzensiz bir şekle sahip olması bir problemdi. Her ne kadar ağırlığı bilinse de hacmi bilinmiyordu.
Arşimet’in, bir kap içindeki suyun seviyesinin, içine bir kilogram altın atılmasıyla ne kadar yükseleceğini ölçtüğü; böylece bunu bir kilogramlık gümüşle tekrarlayarak her iki sonucu kıyasladığı biliniyor. Deneyi yapan Arşimet, bir kilogramlık gümüş suya batırıldığında, aynı ağırlıktaki altından daha fazla su taşırdığını keşfetmiştir.
Bunun sebebi ise aynı ağırlığa sahip olan gümüş, altına kıyasla daha fazla hacme sahiptir. Deneyine devam eden Arşimet, bu sefer tacı suya batırır ve taşan suyu, taç ile aynı ağırlıkta olan altının taşırdığı suyla kıyaslar.
Bunun üzerine tacın, aynı ağırlıktaki altından daha fazla su taşırdığını fark eder. Böylece altın ve gümüşün bir karışımı olduğunu bularak ne kadar altının çalındığını söyleyebilmiştir. Kral için kötü, usta için ise daha kötü bir haber!
Arşimet Vidası
Arşimet vidası ya da diğer ismiyle su vidası, çağlar boyunca günümüze kadar gelen basit bir makinedir. Tarihçiler, Arşimet vidasının kullanımına ilişkin ilk kanıtın, Milattan önce 250 yılından geldiğini söylüyor.
Bu alet Arşimet’in ismini almıştır. Çünkü O’nun tarafından icat edildiği düşünülüyor. Fakat arkeolojik kanıtlar, aletin daha önceden Mısır ya da Asur’da(günümüz Irak toprakları) icat edilmiş olabileceğine işaret ediyor. Buna göre Arşimet sadece önceki tasarıma dayanarak aleti geliştirmiştir diyebiliriz.
Arşimet vidası, iki yaygın basit makinenin birleşimini temsil ediyor: Eğimli düzlem ve silindir. Düzlem, silindirin etrafını sararak tipik bir vida şeklini meydana getiriyor. Ancak Arşimet vidasının amacı herhangi bir şeyi delmek değildir.
Daha ziyade vidanın dönüşü, sıvıyı ya da küçük maddeleri yukarıya doğru harekete zorlar. Bu hareketin sonucu olarak da sıvıyı işlemesi, sulama yapması ve suyun kuyudan çıkarılması gibi birçok işlevi yerine getirmesi amaçlanır.

Arşimet Pi (π) Sayısını Hesaplıyor
π sayısını, bir çemberin çevresini, çapına böldüğünüz zaman elde edersiniz. Çemberin alanını ya da çevresini hesaplamak için π sayısını bilmeniz gerekir.
Arşimet silindir, küre ve koni gibi geometrik cisimlerin matematiksel özelliklerini hesaplama konusuna özel bir ilgi gösteriyordu. Bunu yapabilmesi için de π sayısı hakkında daha fazla şey öğrenmek istedi.
π sayısının bir rasyonel sayı olduğunu biliyoruz. Tam olarak söylemek gerekirse 3.14159265358979… şeklinde sonsuza kadar gidiyor. Bu yüzden tam değerini bulmak matematikçiler açısından imkansızdır.
Arşimet bir çemberin çevresinin 2 x π x r’ye eşit olduğunu biliyordu. Buradaki “r” ifadesinin çemberin yarıçapı olduğunu belirtelim. Böylece yarıçapı bilinen bir dairenin çevresini hesaplayan Arşimet, π sayısını da bulmuş oluyordu.
Bu yönteme the method of exhaustion ya da “tüketme yöntemi” denir. Yaklaşık bir yüzyıl önce Eudoxus tarafından geliştirilmiştir. Öklid ise “Elementler” adlı eserinde altı tane önermesini kanıtlamak için bu yöntemi kullanmıştır.
Arşimet bir çemberi düşündü. İçine ise eşkenar bir üçgen çizdiğini farz etti. Bu üçgenin her köşesi ise çembere dokunuyordu. Çemberin dışında ise diğer bir eşkenar üçgen çizdi. Bu üçgen daha büyük olup her kenarı içteki çembere dokunuyordu.
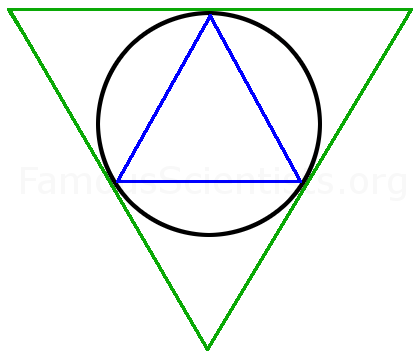
Her üçgenin çevresini kolay bir şekilde hesaplayan Arşimet, böylece çemberin çevresinin içteki üçgenden daha büyük, dıştaki üçgenden daha küçük olduğunu buldu.
Arşimet sonra çemberin içine ve dışına birer kare yerleştirdi ve aynı işlemi tekrar yaptı. Sonra beşgen, altıgen, yedigen… şeklinde devam etti. Örneğin çemberin içine küçük bir düzgün altıgen, dışına da daha büyük bir düzgün altıgen yerleştirdi. Altıgenin, çemberi üçgenlere göre daha fazla kapsadığını fark etti. Altıgenin çevreleri, çemberin gerçek çevresine daha yakındı.
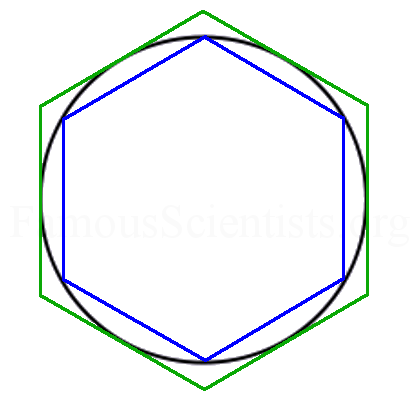
Arşimet işte bu şekilde bir çemberin çevresine iyice yaklaşacak şekilde düzgün çokgenler kullanarak işleme devam etti. Son olarak, çemberin içinde ve dışında 96 kenarlı bir düzgün çokgenin çevresini hesapladı. 96 kenarlı düzgün bir çokgen, büyüteçle bakılmadığı sürece bir çember ile neredeyse aynı gözüküyordu.

Çokgen mi Çember mi ?
96 kenarlı çokgeni kullanarak, Arşimet π sayısının 3.1408 ve 3.1429 arasında bir sayı olduğunu buldu. Eğer bulduğu bu sayıyı ortalama bir değer olarak verirsek, Pi sayısını 3.141868115 olarak bulmuştur. Bulduğu bu değer, hesap makinelerindeki değerden sadece 10000’de 1 farklılık gösteriyor!
Şunu da hatırlatmakta fayda var. Arşimet yaptığı hesaplar için gerçek ölçümler yapmamıştır. Eğer yapsaydı yeteri kadar kesin değerlere ulaşamazdı. Şekillerin alanını hesaplamak için yalnızca zihin gücünü kullanmıştır.
Kürenin Hacmini Hesaplama
Arşimet, küre gibi bir cismin yaklaşık hacmini, küreyi bir dizi küçük silindire bölüp, ortaya çıkan bu silindirlerin hacimlerini toplayarak hesaplamıştır. Bu silindirleri daha da ince olacak şekilde bölerek, yaklaşımının gerçek değere daha yakın olduğunu fark etmiştir.
İşte böyle tam doğru bir hesaplamaya ulaşır. Modern integral kalkülüse benzer bir şekilde, sonsuz küçükler serisini kullanarak bu tarz problemleri çözüme kavuşturmuştur.
Belki de Arşimet, bütün antik Yunan matematikçileri arasında, sonsuzluk kavramına ilişkin en ileri görüşe sahiptir. Yunanlar’ın kesin, katı kuralları tercihi ve paradokslara karşı güvensizliği, onların tamamen “gerçek sonsuzluk” kavramından kaçındığını gösteriyor.
Öklid bile, asal sayıların sonsuzluğuna ilişkin kanıtında, “potansiyel olarak sonsuz asal sayı vardır” derken bile dikkatli davranmıştı. “Gerçek sonsuz” yerine “potansiyel” sözcüğünü tercih etmişti.
Ancak Arşimet Parşömeni’nde Arşimet, gerçek sonsuzluğun olma ihtimalinden tarihte ilk defa bahseden kişidir.
Arşimet’in hesaplamadaki titizliği ve hassaslığına ilişkin diğer bir örnek ise 3 sayısının karekökünü hesaplamasıdır. Bu değerin yaklaşık 1.7320261 – 1.7320512 arasında olduğunu hesaplamıştır.
Bununla da yetinmeyen Yunan matematikçi, bütün evreni doldurmak için gereken kum tanelerinin sayısını da hesaplamıştır. Bulduğu değer ise 8 vigintillion, yani yaklaşık 8 x 10^63( 8 çarpı 10 sayısının sağına 62 tane sıfır) idi.
Arşimet’in Fizik Kanunlarına Bakışı
Keşfettiği bütün fiziksel kanunlara rağmen, Arşimet asla onları “kanun” olarak nitelememiş, ölçüm ve gözlemler şeklinde onları tanımlamamıştır. Bunun yerine bu kanunlara, saf matematiksel teoremler olarak bakmıştır. Öklid’in geometri için geliştirdiğine benzer bir mantık sistemini Arşimet’in de kullandığını söyleyebiliriz.
Arşimet’in zamanında Yunan biliminin, gözlemlere az değer verme ve mantıksal argümanları önemseme gibi bir eğilimi vardı. Yunanlar, en üstün bilginin tümdengelimci sorgulamaya dayandığına inanıyordu.
Ancak bu, Arşimet’i deney yapmaktan alıkoymamıştı. Aslında çağdaşlarından bu noktada ayrılıyor Arşimet. Çünkü sahip olduğu teorik bilgisini pratik alana başarılı bir şekilde uygulamıştır.
Fakat keşiflerini sunma yöntemi her zaman matematiksel bir bakış açısından geliyordu. Hiçbir şekilde mühendislik tarzında sistematik bir tanım verme girişiminde bulunmamıştır. Dahası mekanik deneylerden bahsettiği zamanlarda, aslında onları matematiğin anlaşılmasına yardım etmek için kullanmıştı.
Arşimet’in bu yöntemi, antik dönem bilimi ile modern dönem biliminin yaklaşımları arasındaki önemli bir farkı gözler önüne seriyor. Antik dönem bilimi açısından deneyler, teorik bir anlayışa ulaşmak için kullanılırken modern bilimde teoriler, deneysel sonuçlara ulaşmak için kullanılıyor.
Arşimet : Bana Bir Kaldıraç Verin, Dünyayı Yerinden Oynatayım!
Arşimet’e atfedilen ünlü bir söz vardır:
Üzerinde duracağım bir yer verin ve Dünya’yı yerinden oynatayım.
Arşimet’in bahsettiği şey kısaca şudur: Eğer bir destek noktasına ve yeteri kadar uzun bir kaldıraca sahip olsaydı, Dünya’yı yerinden oynatabileceğini iddia ediyordu.
Tabi ki bu cümleyi söylemesinin amacı, denge prensiplerini bulmuş olmasıdır. Arşimet’in bulduğu söylenen denge prensipleri ise şunlardır:
- Eşit kollu terazide asılı duran ağırlıklar dengede kalmaya devam eder.
- Eşit ağırlığa sahip olmayan ağırlıklar, eşit olmayan kollarda belirli şartlarda dengede kalır. Bu şart ise şudur : F1 x a = F2 x b
Öte yandan kütleçekim merkezine ilişkin çalışmaları da mekanikteki yaşanacak gelişmeler için çok önemliydi.
Arşimet ve Gurur Duyduğu Keşfi
Arşimet’in en gururlu olduğunu iddia ettiği keşfi, bir küre ve aynı yükseklik ve çapta olan, etrafını kaplayan bir silindir arasındaki ilişkiydi. Kürenin alanını 4⁄3πr3 olarak, aynı yükseklik ve çaptaki silindirin alanını ise 2πr3 olarak hesaplamıştır. Kürenin yüzey alanı ise 4πr2 olup, silindirin yüzey alanı 6πr2‘dı.
Bu nedenle kürenin, silindirin hacminin üçte ikisine eşit bir hacme sahip olduğu ortaya çıkıyor. Aynı zamanda kürenin yüzey alanının da silindirin üçte ikisi olduğunu söyleyebiliriz. Arşimet bu sonuç karşısında o kadar keyif almış olacak ki mezar taşına bu iki şeklin bir kalıbının yapılmasını vasiyet etmiştir.
Arşimet’in Ölümü
Kral II.Hiero’nun ölümünden sonra Siraküza ve Roma arasında bir savaş meydana geldi. Siraküza şehri hem karadan hem de denizden saldırıya uğramıştı. 75 yaşında olmasına rağmen Arşimet, şehrini savunmaktan geri durmamıştır. Bir mühendis kafasına sahip olan Arşimet, bu bilgilerini kullanarak uzak mesafelere ağır taşlar fırlatan mancınıklar geliştirmişti.
Bu fırlatılan taşlar, şehir duvarlarında delikler açarak okçuların ok atabilmesine imkan sağlıyordu. Ayrıca, Roma gemileri yeteri kadar yakına geldiği zaman üzerlerine çok ağır taşlar bırakabilen vinçlere yardım ediyordu.
Bu icatlar o kadar etkili olmuş olacak ki Romalı kumandan Marcus Claudius Marcellus, Siraküza şehrine saldırma fikrinden vazgeçer ve şehri düşürmenin tek yolunun bir kuşatma olacağına karar verir. Böylece Milattan önce 212 yılında, kuşatmanın etkisiyle kıtlık başlayan Siraküza şehri teslim olur ve Romalılar burayı ele geçirir.
Marcellus’un, Arşimet’in zekasından çok etkilendiği ve canlı ele geçirilmesi emrini verdiği söylenir. Bunun üzerine Romalılar Arşimet’i, kumun üzerinde geometrik şekiller çizerken bulur. Arşimet askerlerin verdiği emirlere uymaz ve çalışmalarını bitirmesi için fazladan zaman ister. Umursanmayan askerler sinirlenerek, tarihin en büyük dehalarından birisini oracıkta öldürmüştür.
Kaynaklar:
1- Ancient History Encyclopedia, “Archimedes”, (Alındığı Tarih : 12 Mart 2021), Ancient History Encyclopedia
2- Famous Scientists, “Archimedes”, (Alındığı Tarih : 12 Mart 2021), Famous Scientists
3- The Story Of Mathematics, “Who Was Archimedes”, (Alındığı Tarih: 13 Mart 2021), The Story Of Mathematics
4- Thomasnet, “The Archimedes Screw”, (Alındığı Tarih: 13 Mart 2021), Thomasnet
5- Wikipedia, “Method of Exhaustion”, (Alındığı Tarih: 13 Mart 2021), Wikipedia