Harezmi (780 – 850), ilk dönem İslam filozoflarından birisi olup aynı zamanda bir matematikçi ve astronomdur. En çok Hint-Arap sayılarını ve “cebir” kavramını Avrupa’ya ve tüm dünyaya tanıtmasıyla bilinir. Bu yönüyle Harezmi, yaptığı çalışmalarla birçok bakımdan bilim tarihinde büyük bir etki bırakmıştır.
Bugün bile onun geliştirdiği onluk sayı sistemini ve matematikteki cebir yöntemini kullanmaktayız. Harezmi’nin isminin Latince versiyonu olan Alkhorizmi, bugün kullandığımız “algoritma” ifadesinin ve en bilinen eseri olan Kitāb al-mukhtaṣar fī ḥisāb al-jabr wal-muqābala(Tamamlama ve Dengeleme ile Hesaplama Üzerine Özlü Kitap) kitabındaki al-jabr ifadesi de matematikteki “cebir” kelimesinin kökenlerini oluşturmaktadır.
Harezmi’nin hayatına ilişkin çok fazla bilgi bulunmamakla birlikte, yalnızca İslam bibliyografik çalışmalarından ve İslam tarihçi ya da coğrafyacılarından aktarılan detaylarla özel hayatı hakkında sınırlı bir bilgi birikimine sahibiz. Gerçek ismi Ebû Ca’fer Muhammed bin Mûsâ el-Hârizmî olup el-Harezmi lakabının, Harezmi’nin muhtemelen o zamanlar Harezm bölgesinden, bugünkü Özbekistan’ın Hive kentinden gelmesi dolayısıyla verildiği söyleniyor. Harezmi Türk mü Fars mı sorusuna vereceğimiz cevap Harezmi’nin köken olarak Türk olduğudur.
Harezmi’nin Hayatı ve Tarihsel Bağlam
10.yüzyılda İslam halifesi olan el-Memun, hızla genişlemekte olan Abbasi İmparatorluğu’nu başkent Bağdat’tan yönetmekteydi. Babası Harun Reşid tarafından başlatılan büyük çaplı öğrenim faaliyetini devam ettiren Memun, Beyt-ül Hikme(Bilgelik Evi) isimli bir akademi kurmuştu.
O dönemde Beyt-ül Hikme’de yapılan şey çoğunlukla Antik Yunan dönemine ait felsefi ve bilimsel çalışmaların tercüme edilmesiydi. Müslümanlar Antik Yunan filozoflarının çalışmalarına o kadar aşina olmuşlardı ki o zamanlar Aristoteles‘i “büyük muallim” olarak bile nitelemişlerdi.
El-Memun, Beyt-ül Hikme’yi kurmakla kalmayıp, eski dönemlere ait bir sürü el yazmaların bulunduğu bir kütüphane de kurmuştu. Bu kütüphane, Eratosthenes‘in de müdürlüğünü yaptığı İskenderiye Kütüphanesi’nden bu yana kurulmuş en büyük kütüphaneydi. Ayrıca Halife, gözlemevleri de kurarak Müslüman astronomların, daha önceki Antik Yunan astronomisi ve diğer kültürlerin astronomik çalışmaları üzerine daha kapsamlı çalışmalar yapabilmesine olanak sağlıyordu.
Bağdat, 9.yüzyıl itibariyle ticaretin ve bilimsel araştırmaların merkezi olmuştu. Çin ve Hindistan gibi uzak diyarlardan gelen birçok tüccar ve bilim insanı bu şehre göç ediyordu. Bilim ve araştırmaya çok meraklı olan Harezmi de entelektüel faaliyetlerini gerçekleştirmek amacıyla Bağdat’a gitmeye karar vermişti. Burada çalışmalarına devam ederken Halife Memun’un, Harezmi’nin bilgin bir kişi olduğunu fark etmesi üzerine onu, Beyt-ül Hikme’de alim olarak çalışmak üzere görevlendirdi.

Antik Dünya Bilim İnsanları adlı eserinde Margaret J.Anderson şöyle diyor:
Harezmi Bağdat’a geldiği zaman henüz yeni bir şehir sayılırdı. Fakat ticaret rotalarının merkezinde olan konumu ve Akdeniz’de sahip olduğu limanlar, şehrin hızlı bir şekilde büyümesine sebep olmuştu. 813’ten 823’e kadar Bağdat, halife El-Memun tarafından yönetildi. Kendisi de meraklı bir alim ve filozof olan Memun, çok geçmeden şehri önemli bir entelektüel merkeze çevirmişti. Beyt-ül Hikme’yi kurarak, Harezmi gibi himayesindeki alimleri klasik Yunan metinlerinin Arapça’ya tercüme edilmesi konusunda görevlendirdi. Bu kitapların kopyaları ise İspanya ve Sicilya başta olmak üzere Avrupa’da da Müslümanlara ait birçok öğrenme merkezinin ortaya çıkmasına sebep oldu. Latince’ye çevrilen bu eserler, Avrupa’daki bütün üniversitelere ulaşmıştı.
Harezmi ve çalışma arkadaşlarının görevi de Antik Yunan el yazmalarının tercüme edilmesiydi. Bunun yanı sıra cebir, geometri ve astronomi üzerine de çalışmalar gerçekleştiriyorlardı. Harezmi, çalışmaları sonucu yazdığı “Hisab al-jabr w’al-muqabala“(Tamamlama ve Dengeleme ile Hesaplama Üzerine Özlü Kitap) isimli eserini Halife’ye adamıştı. Bu kitap, Harezmi’nin en ünlü ve önemli eserleri arasında bulunur. “Cebir” ifadesinin de kökeni olan bu kitap, ikinci dereceden denklemler üzerine yazılmış tarihteki ilk kitap olarak bilinir.
Harezmi’nin Matematiğe Katkıları
Harezmi’nin Cebir kitabı, genel olarak temel matematik problemlerinin ele alındığı bir eserdir. Genellikle miras, dava, ticaret, arazi ölçümü gibi konularda ortaya çıkan matematiksel problemler ile ilgilenir. Bu bağlamda Cebir kitabının daha çok pratik hesaplamalar ve ölçümler ile ilişkili olduğunu söyleyebiliriz.
Her ne kadar kitabın daha çok pratik amaçlara yönelik yazıldığı görülse de Harezmi cebir ifadesini, o dönemdeki İslam İmparatorluğu’nda yaşayanların günlük hayatlarının bir parçası olan gerçek problemleri çözmek üzere tanıtmıştır. Harezmi, kitabın ilk bölümlerinde doğal sayıları, rakamlar yerine bir takım sözcükler üzerinden tanımlıyor. Kendi ifadesiyle:
İnsanların genel olarak hesaplamak istedikleri şeyi düşündüğüm zaman, bunların bir sayı olduğunu görüyorum. Ayrıca her sayının “birimlerden” oluştuğunu ve birimlere bölünebileceğini gördüm. Dahası, 1’den 10’a kadar ifade edilebilen her sayının, kendinden öncekinin bir birim fazlası olduğunu; on sayısının tıpkı önceki birimler gibi ikiye ve üçe katlanabileceğini fark ettim. Böylece yüz sayısına gelene kadar yirmi, otuz gibi sayılar da ortaya çıkar. Sonra yüz sayısı da aynı şekilde birimler ve onlar gibi, ikiye ve üçe katlanarak bine kadar gider. Bu şekilde de sayılar devam eder.
Harezmi’nin kitabı, her ne kadar günümüzde kullanılan cebirsel ifadelere yer vermese de modern cebrin temel kitabı olarak görülüyor. O, problemleri açıklamak üzere sayılar yerine kelimeler kullanmıştı. Fakat kitap, ikinci derece denklemler gibi ifadeleri çözmek üzere bir tüketme yöntemi sağlamaktadır. Ve tarihte ilk defa indirgeme(bir ifadeyi daha basit biçimde tekrar yazma), tamamlama(negatif bir niceliği denklemin bir tarafından diğer tarafına alma ve işaretini değiştirme) ve dengeleme(bir denklemin her iki tarafından aynı niceliği çıkarma ve karşıt taraflardaki benzer terimlerin birbirini götürmesi) isimli 3 tane temel cebirsel yöntemi tanıtmıştır.
Örneğin Harezmi’nin kendi verdiği örneklerden yola çıkarak cebir, x.x = 40x – 4x.x ifadesini 5x.x = 40x ifadesine dönüştürür. Al-muqabala ifadesi “dengeleme” anlamına gelir ve benzer terimlerin birbirini götürmesini amaçlar. Örneğin 50 + 3x + x.x = 29 + 10x ifadesini 21 + x.x = 7x ifadesine dönüştürür.
Özellikle Harezmi, herhangi bir denklemi altı tane standart formun birine indirgemek üzere, tamamlama ve dengeleme yöntemlerini kullanarak ikinci derece denklemleri sistematik olarak çözmek için bir formül geliştirmişti. Bu standart formları “kareler”(x2), “kökler”(x), ve sayılar olarak tanımlayarak şöyle ifade eder:
- Kareler köklere eşittir(ax2 = bx).
- Kareler sayılara eşittir(ax2 = c).
- Kökler sayılara eşittir(bx = c).
- Kareler ve kökler sayılara eşittir(x2 + 10x = 39).
- Kareler ve sayılar köklere eşittir(x2 +21 = 10x).
- Kökler ve sayılar karelere eşittir(3x+4 = x2).
Harezmi sonrasında altı standart denklem tipinin nasıl çözüleceğini gösteriyor. Çözümü ifade ederken hem cebirsel hem de geometrik yöntemler sunuyor. Örneğin x2 + 10x = 39 denklemini şu şekilde ifade ediyor:
Bir kare(x2) ve on kök(10x) 39 birim eder. Böylece bu denklem tipindeki soru şu şekildedir: On köküyle(10x) toplanınca otuz dokuz sonucunu verecek olan sayının karesi(x2) nedir?
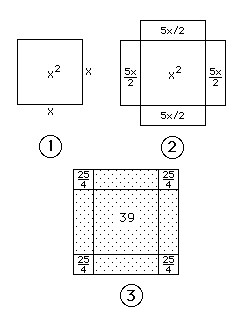
Harezmi bu denklemi çözmek için yukarıdaki görselde de görüldüğü üzere bir geometrik kanıt kullanır. Öncelikle x kenarlı bir kare ile başlar. Böylelikle karenin alanından denklemdeki x2 ifadesi elde edilir. 10x kökünü eklemek için karenin kenarlarına, uzunluğu x ve genişliği 5/2 olan dört tane dikdörtgen eklenir. Böylece ikinci şeklin alanı x2 + 10x eder ki bu da 39’a eşittir.
Daha sonra büyük kareyi, her birinin alanı 25/4 olan dört tane küçük kare ekleyerek tamamlar. Bu küçük karelerin alanının toplamı da 25 yapar. Bu nedenle üçüncü şekildeki büyük karenin alanı 25 + 39 işleminden 64 eder. Demek ki üçüncü şekildeki büyük karenin bir kenarı 8 birim uzunluğundadır. Köşelerdeki küçük karelerin bir kenarının 5/2 ve dikdörtgenin bir kenarının x olduğunu biliyoruz. O halde 5/2 + 5/2 + x = 8 işleminden x ifadesinin 3 çıktığını rahatlıkla görebiliriz.
Bu geometrik kanıtlara bakarak uzmanlar arasında ise birtakım tartışmalar sürüyor. Tartışmanın kaynağı ise Harezmi’nin, ünlü Antik Yunan matematikçisi Öklid‘in Elementler eserinden haberi olup olmadığıdır. Harun Reşid’in hükümdarlığında Haccac Bin Yusuf’un, Öklid’in Elementler kitabını Arapça’ya çevrildiği biliniyor. Haccac, Beyt-ül Hikme’de Harezmi’nin çalışma arkadaşı olduğu için Harezmi’nin, Öklid’in bu kitabını okumuş olabileceği yorumu yapılabilir.
Harezmi’nin Astronomi Alanında Yaptığı Çalışmalar
Harezmi’nin astronomi alanında yaptığı çalışmalarını derlediği eser Zic-el-Sindhind ismiyle bilinir. 770 yılında Hintli bir heyetin, Bağdat’a ziyareti esnasında Halife El-Mansur’un sarayına getirttiği Sanskritçe yazılmış bir astronomik çalışmaya dayanan bu eser, aslen Hint astronom Brahmagupta’nın Brāhmasphutasiddhānta isimli eserinin bir çevirisidir.
Mansur’un emriyle Arapça’ya çevrilen esere Zic al-sindhind ismi verilmiştir. Zic, kelime anlamı itibariyle astronomik tabletler manasına gelirken sindhind, Sanskritçe olan siddhānta kelimesinin değiştirilmiş bir halidir.
Harezmi’nin çalışması ise aslında Zic al-sindhind eserini yeniden ele almaktadır. Bu çalışma, günümüze kadar gelen ilk Arapça astronomik eser olması bakımından büyük önem arz ediyor. Harezmi’nin çalışması, hesaplama ve tabletlerin kullanımı için talimatlardan oluşurken, Batlamyus tarafından standart hale getirilenlere çok benzeyen tabletler de içeriyor.
Güneş, Ay ve o dönemde bilinen beş gezegenin her birinin hareketlerine ilişkin tabletler içeren bu eserde aynı zamanda Güneş ve Ay tutulmaları, gök cisimlerinin enlem ve boylam bilgileri ve çeşitli trigonometrik tabletler de bulunuyor.
Her ne kadar Batlamyus’un astronomik tabletleri, Harezmi ve Fergani gibi diğer Müslüman astronomların çalışmalarını etkilemiş olsa da Harezmi’nin tabletlerindeki temel parametrelerin çoğunun Hint astronomisinden alındığını görüyoruz. Harezmi’nin 7 gök cisminin hareketleri, konumları, Ay’ın Dünya’ya en uzak olduğu konum ve düğüm noktalarına yönelik verdiği bilgilerin hepsi de Brahmagupta’nın eserlerinde verdiği bilgilerle büyük benzerlik taşıyor.
Harezmi, ekliptiğin eğimini belirlemek üzere Bağdat’ta yapılan gözlemler hakkında da birtakım görüşler beyan etmişti. Ekliptiğin eğimini ölçmeye yönelik daha öncesinde Hipparkos gibi Antik Yunan dönemi astronomları birtakım girişimlerde bulunmuştu. Daha sonrasında İslam döneminde yaşamış alimler de öncesinde elde edilen verileri iyileştirmek adına ölçümler yapmıştı. Harezmi’nin döneminde Müslüman astronomların bulduğu değer 23° 33′ idi. Harezmi ise ekliptiğin eğimi için 23° 51′ değerini bularak, her ne kadar diğerlerininki kadar olmasa da oldukça hassas bir gözlem yapmıştır.
Harezmi’nin günümüze kadar ulaşan diğer bir çalışması ise Yahudi takvimi üzerine yazdığı kısa bir eser olan Istikhrājt’rikh al-yahūd (Yahudi Dönemi’nin Çıkarılması) adlı çalışmasıdır. Bu konuya olan ilgisinin, Harezmi’nin aynı zamanda bir astronom olduğu düşünülürse oldukça normal olduğunu söyleyebiliriz.
Eser, genel olarak Yahudi takvimini, 19 yıllık Ay döngüsünü, Yahudilikte ayın ilk günü olan Tishri‘nin haftanın hangi gününe geldiğini belirlemek gibi yöntemleri içeriyor. Ayrıca Yahudi takvimini kullanarak Ay’ın ve Güneş’in ortalama boylamlarını belirlemek üzere birtakım kurallar da veriyor. Her ne kadar küçük bir eser olsa da Harezmi’nin bu çalışması, günümüzdeki Yahudi takviminin temel dayanağı olduğu söylenebilir.
Öte yandan Harezmi usturlap üzerine iki kitap kaleme almıştır: Kitāb ‘amal al-asturlāb (Usturlabın Tasarımı Üzerine Kitap) ve Kitāb al-amal bl’l asturlab (Usturlabın Çalışması Üzerine Kitap). Muhtemelen bu ikincisi, 9.yüzyıl astronomu Fergani’nin çalışmasından elde edilen bir alıntıydı. Bu alıntı, usturlabın yardımıyla çeşitli astronomik problemlerin çözümü hakkında malumat veriyordu. Örneğin Güneş’in göksel enlem ve boylamının belirlenmesi ya da bir konumun yeryüzündeki koordinatlarının verilmesi gibi.
Harezmi’nin Coğrafyaya Katkıları
Harezmi’nin Kitāb sũrat al-ard (Dünya’nın Şekli Üzerine Kitap) isimli kitabı neredeyse tamamen şehirlerin ve yerleşim yerlerinin enlem ve boylamlarının bir listesinden oluşur. Kitapta yerleşim yerleri “yedi iklim bölgesine” göre belirleniyordu. Burada şu bilgiyi de verelim ki Antik Yunan döneminde coğrafya alanına ilişkin yapılan birçok çalışmada bilinen dünya, enleme göre “iklim” olarak bilinen yedi bölgeye ayrılmıştı. Her iklim bölgesinin de yılın en uzun gününde, aynı miktarda gün uzunluğuna sahip olması gerekiyordu.
Harezmi’nin enleme göre belirlediği her iklim bölgesi de kendi içinde boylam çizgilerine göre bölünüyordu. Boylamlar ise en uçtaki batı meridyeninden, “batı okyanus kıyısından” itibaren sayılıyordu. Kitabın ilk kısmı şehirleri, ikinci kısmı dağları(uç kısımlarını ve yönlerini), üçüncü kısım denizleri ve kıyılardaki belirli noktaların koordinatlarını, dördüncü kısım adaların uzunluğunu ve genişliğini, beşinci kısım ise çeşitli coğrafi bölgelerin merkez noktalarını, altıncı kısım nehir ve ırmakların kaba bir tanımını veriyordu.
Harezmi’nin bu çalışması ve Batlamyus‘un Coğrafya adlı eseri arasında birtakım benzerlikler olduğunu söyleyebiliriz. Coğrafya, dünya haritasının bir tasvirini ve harita üzerinde bölgelere göre ayrılmış önemli yerlerin koordinatlarının bir listesini veriyordu. Batlamyus’un bu eserinde listelenen yerlerin çoğunun ayrıca Harezmi’nin eserinde de kullanıldığını görebiliyoruz.
Fakat Harezmi’nin eseri, Batlamyus’un kitabının yalnızca bir çevirisi ya da uyarlamasından daha fazlasıdır. Harezmi tarafından yapılan haritanın planı bariz bir şekilde farklı olup iklim bölgeleri açısından da Batlamyus’un belirlediğinden önemli ölçüde farklılık gösterir.
Harezmi’nin çizdiği haritalar, birçok bakımdan Batlamyus’un haritalarından daha doğrudur diyebiliriz. Özellikle de o dönemde Abbasi İmparatorluğu’nun hakimiyetindeki coğrafi bölgeler, Harezmi tarafından daha hassas bir biçimde belirlenmişti. Fakat Harezmi’nin haritasındaki en önemli gelişme, Batlamyus’un Akdeniz’in büyüklüğüne ilişkin abartılı tasvirlerini normale yakın olarak vermesiydi.
Ayrıca Afrika ve Uzak Doğu bölgelerine yönelik bazı bozulmaları da Harezmi’nin düzelttiği bilinmektedir. Fakat Avrupa kıtası konusunda Harezmi, Batlamyus’un haritalarından daha doğru bir tasvir verememiştir. Örneğin Atlantik denizinin kuzeyde Avrupa’ya bağlanan bir kıta tarafından çevrili bir iç deniz olduğunu belirtiyordu.
Hint Rakamları
Harezmi aynı zamanda Hint-Arap sayıları üzerine bir çalışma kaleme almıştı. Bu eserin Arapça orijinali kayıp olmakla birlikte Latince çevirisi olan Algoritmi de numero Indorum(Harezmi Hint Sayma Sanatı Üzerine), Harezmi’nin isminin Latince versiyonu olan Al-Khourismi’den “algoritma” kelimesinin çıkmasına sebep olmuştur. Ne yazık ki eserin Latince çevirisinin Harezmi’nin orijinal eserine kıyasla çok fazla değiştiğini söyleyebiliriz.
Kitap, 1, 2, 3, 4, 5, 6, 7, 8, 9 ve 0 rakamlarına dayanan Hint ondalık basamak sayı sistemini tanımlamaktadır. 0 rakamından İslam coğrafyasında ilk defa bu eserde bahsedildiğine dayanarak, Harezmi 0 rakamını ilk kullanan Müslümandır diyebiliriz. Bunun yanı sıra karekökleri bulmak üzere geliştirilen yöntemlerinde eserin Arapça orijinalinde olduğu bilinmektedir. Fakat Latince versiyonunda bunu görememekteyiz.
Bunun yanında Harezmi, sinüs fonksiyonlarını içeren, daha sonrasında tanjant fonksiyonlarını da kapsayan detaylı trigonometrik tabletler de geliştirmişti. Sonuç olarak Harezmi’nin birçok kitabı Latince’ye çevrilmiş ve 16.yüzyıla kadar Avrupa üniversitelerinde temel matematik ders kitabı olarak kullanılmıştır.
Harezmi’nin Eserleri ve Avrupa’ya Etkileri
Harezmi’nin gerçekleştirdiği bilimsel başarıların birçok bakımdan temel seviyede olduğunu söyleyebiliriz. Lakin sonraki nesillerde yarattığı etki yadsınamayacak boyuttaydı. Harezmi, entelektüel çalışmalarını yapabileceği çok müsait bir dönemde yaşamıştı. Çünkü bilim, dönemin halifeleri tarafından desteklenmiş; aynı zamanda İslam medeniyeti Yunan ve Hint bilimine ilgi göstermeye başlamıştı.
Her ne kadar Müslümanlara ait bilimsel çalışmaların çoğu Harezmi’den sonraki dönemlerde ortaya çıkacaksa da bu dönemde yapılan tercüme faaliyetleri de büyük bir entelektüel oluşuma zemin hazırladı. 9. ve 10. yüzyıllarda cebir kavramı İslam topraklarında daha fazla geliştirildi. Fakat El-Kereci ve Ömer Hayyam gibi ileri seviye matematikçiler bile Harezmi’nin cebire ilişkin retorik ifadelerini kullanmayı tercih etmişti.
Harezmi’nin Cebir adlı eseri daha sonraki dönemlerde ders kitabı olarak Avrupa’da kullanılmaya devam etmiştir. Hint sayı sistemi hakkında yazdığı eser ise İslam topraklarında bilinmekle birlikte en büyük başarısını, 12.yüzyılda Latince çevirileriyle birlikte Batı’ya tanıtılınca elde etmiştir. Hatta Harezmi’nin ismi, Hint sayılarının kullanıldığı “yeni aritmetik” kavramıyla o kadar yakından ilişkili olmuştu ki isminin Latince versiyonu olan algorismus, aritmetik üzerine yazılan her kitabın adına veriliyordu.
Astronomi ile alakalı Harezmi’nin bir diğer çalışması olan Zic-el-Sindhind ise uzun dönemler boyunca kullanılmaya ve çalışılmaya devam etmiştir. Yaklaşık 900 yılında Battani, Batlamyus’un Almagest eserine ve kendi gözlemlerine dayanarak büyük astronomik çalışmasını yayımlamıştı. Bu eser, neredeyse her alanda Harezmi’nin çalışmasından üstün olmasına rağmen Harezmi, bu alanda çalışmalar gerçekleştiren ilk Müslüman olması bakımından kendisinden söz edilmeyi hak ediyor.
Harezmi’nin coğrafya alanındaki Kitāb sũrat al-ard adlı eseri de özellikle İslam topraklarında çok fazla kullanılmıştı. Hatta Batlamyus’un ünlü Coğrafya eseri Arapça’ya çevrildiği dönemlerde bile Harezmi’nin bu eseri çok fazla rağbet görüyordu. Fakat birtakım müphem sebeplerden ötürü Harezmi’nin coğrafya alanındaki eseri Avrupa’da 19.yüzyıla kadar bilinmiyordu. Buna rağmen kitapta içerilen bilgilerin bazıları Ortaçağ Avrupası’na, önde gelen şehirlerin antik ve Ortaçağ astronomik tabletlerine işlenmiş olan enlem ve boylam bilgileri yoluyla ulaşmıştı.
Kaynaklar:
1- Famous Scientists, “Muhammad ibn Musa al-Khwarizmi“
2- Mactutor, “Al-Khwarizmi(790-850)“
3- Story of Mathematics, “MUHAMMAD IBN MUSA AL-KHWARIZMI: MUSLIM MATHEMATICIAN“
4- New World Encyclopedia, “Muhammad ibn Mūsā al-Khwārizmī“
5- Encyclopedia, “Al-Khwārizmī, Abū Ja’far Muhammad Ibn Mūsā“
6- History of Islam, “Al Khwarizmi“
7- Matematiksel.org, “El Harezmi: Medeniyetler Arasında Bir Köprü“
8 – Britannica, “Al-Khwārizmī“