Galileo’nun Eğik Düzlem Deneyi ve Hareket Yasaları

Hareket olgusu, evrenimizin en temel gerçekliklerinden birisidir. Maddenin bulunduğu yerde hareketin olmadığı bir durum var mıdır bilinmez. Büyük galaksi kümelerinden galaksilere, yıldızlardan gezegen ve uydulara, moleküllerden maddenin en temel yapı taşları olan atom ve atom altı parçacıklara kadar bildiğimiz her şey hareket halindedir.

Tarih öncesi çağlarda yaşayan insanlar, çevresine baktığı zaman maddelerin temel bir harekete sahip olduğunu fark etmişti. Örneğin bir taşı havaya attığımız zaman önünde sonunda yere düşüyordu.

Bunun üzerine Milattan önce 4.yüzılda yaşamış ünlü filozof Aristoteles, gözlemlerinden yola çıkarak maddelerin temelde iki çeşit harekete sahip olduğunu söylemişti: Doğal hareket ve zorunlu hareket.

Aristoteles’e göre doğal hareket, nesnelerin ya da maddelerin evrendeki doğal yerine doğru hareketinden başka bir şey değildi. Taşı attığımız zaman taş yere düşüyordu çünkü taşın doğal yeri evrenin merkezi, yani Dünya’nın merkeziydi. Ya da ateş, yakıldığı zaman yükseliyordu. Çünkü ateşin doğal yeri gökyüzüydü.

Maddelere içkin bir de zorunlu hareketin olduğunu söylüyordu Aristoteles. Zorunlu hareket, cisim harekete zorlandığı zaman meydana geliyordu. Bu durumda cismin hareket hızı, itim kuvveti ile orantılı olmalıydı.

Aristoteles, yere düşen cisimlerin düşme hızının cismin ağırlığı ile orantılı olduğunu söylüyordu. Bir diğer ifadeyle ağır cisimler, hafif cisimlere göre yere daha hızlı düşüyordu.

Aristoteles’in cisim ve hareketlere ilişkin bu görüşlerinin daha Antik Atina döneminde bile sorgulanmaya başladığını söyleyebiliriz.

Aristo’nun ölümünden otuz yıl gibi kısa bir süre sonra Straton, daha yüksekten bırakılan bir taşın zemin üzerinde daha çok bir etkide bulunduğuna dikkat çekiyordu. Bu da demek oluyordu ki taş ne kadar yüksekten bırakılırsa o kadar hız kazanıyordu.

Her ne kadar Straton gibi filozoflar Aristoteles’in görüşlerine karşıt sayılabilecek örnekler verdiyse de yüzyıllar boyunca Aristotelesçi fizik anlayışı dünyada baskın görüş olmuştu.

İnsanlar, ağır cisimlerin yere daha hızlı düştüğü şeklinde yanlış bir inanca sahipti. Ancak 16.yüzyıla gelindiğinde hareket ya da mekanik bilimi alanında yapılan çalışmalar da belli bir hız kazanmaya başlayacaktı.

Hareket olgusuna ilişkin çalışmalar gerçekleştiren bilim insanları, düşen cisimlerin hareketini daha dikkatli bir şekilde incelemeye başlamıştı. Bu bilim insanlarından birisi de ünlü İtalyan fizikçi ve astronom Galileo Galilei‘dir.

Galileo Galilei Yerleşik İnancı Sorguluyor

En çok yaptığı teleskop gözlemleriyle tanınan Galileo Galilei, astronomi alanında Güneş Merkezli Evren Modeli’nin geçerli bir model olmasında çok önemli bir rol oynamakla bilinmektedir.

Ancak astronominin yanında fizik alanında yaptığı çalışmalarla, modern fizik anlayışımızda bir devrim yaratacak ve Newton’un ünlü hareket yasalarının formüle edilmesinde çok büyük bir pay sahibi olacaktı.

Galileo öncelikle Aristoteles’in ağır cisimlerin hafif cisimlerden daha hızlı yere düştüğü iddiasını ele aldı. Bu iddiayı çürütmek amacıyla bir düşünce deneyine başvurduğu söylenir. Bu düşünce deneyine göre biri ağır, diğeri de hafif olmak üzere iki taş birbirine bağlanır.

Normalde Aristoteles’e göre ağır olan taş, hafif olandan daha hızlı düşeceği için, bağlı halde düşerlerken ağır taşın daha aşağıda düşmesi gerekir. Öte yandan ağır taş ile hafif taşın ağırlığının toplamı, ağır taşın ağırlığından fazla olduğu için bu sefer ikisinin birlikte ağır taştan daha önce düşmesi gerekir.

Görüldüğü üzere bu iki durum birbiriyle çeliştiği için Galileo, ağır cisimlerin hafif cisimlerden önce düştüğü iddiasının doğru olmadığını bir düşünce deneyiyle göstermişti. Buna ek olarak Galileo’nun, hafif cisimler ile ağır cisimlerin aynı anda yere düştüğünü göstermek için Pisa Kulesi Deneyi’ni yaptığı rivayet edilir.

Bu deneyde Galileo, Pisa Kulesi’nin tepesine çıkarak biri hafif diğeri de ağır olan iki taşı aynı anda yere bırakır ve ikisinin de yere aynı anda düştüğüne şahit olur. Ancak bu deneyi yapıp yapmadığı tartışmalı olsa da Galileo, muhakkak ki hafif cisimlerin ağır cisimlerle aynı anda yere düşeceğini biliyordu.

İki Büyük Dünya Sistemi Hakkında Diyalog

1632 yılına gelindiğinde Galileo, astronomi ve fizik alanındaki görüşlerini yansıttığı, hem edebi hem de bilgi verici bir üslup içeren İki Büyük Dünya Sistemi Hakkında Diyalog adlı bir eser kaleme alır.

Adından da anlaşılacağı üzere eserde diyalog tarzı bir anlatım benimseyen Galileo, birbirine zıt görüşler olan Aristotelesçi ve Kopernikçi dünya görüşleri hakkındaki bilgileri üç kişi üzerinden verdiğini söyleyebiliriz.

Sadece astronomi alanında değil, ayrıca hareket ve mekanik konularında da görüşlerini belirtmişti eserinde. Eserin üç karakterinden ikisi olan Salviati ve Sagredo, Galileo’nun görüşlerini yansıtırken Simplicio, tipik bir Aristotelesçiydi.

Galileo’nun diyaloglarda yaptırdığı şey ise her iki dünya görüşünü savunan karakterlerin, inandığı görüş lehine argümanlar sunmasına izin vererek birbirleriyle tartışmalarını sağlamaktı.

Konu cisimlerin hareketine geldiği zaman Galileo ile aynı düşünceleri paylaşan Salviati şunları diyordu:

Aristoteles’in, biri diğerinden 10 kat daha ağır olan iki taşın aynı anda 100 birim bir yükseklikten bırakıldığında, 10 kat ağır olan taşın yere değdiği anda, diğerinin 10 birimden daha fazla düşmediği şeklinde bir deney yaptığından büyük şüphe duyuyorum.

Burada Galileo’nun, Aristoteles’in gerçekten böyle bir deney yaptığından şüphe duyduğunu Salviati üzerinden dile getirdiğini görüyoruz. Simplicio’nun buna cevabı ise Aristoteles’in bu deneyi gerçekten yaptığı şeklindeydi. Bunun üzerine araya Sagredo giriyor ve şöyle diyordu:

Fakat Simplicio, bizzat aynı deneyi yapan biri olarak seni temin ederim ki biri diğerinden çok ağır olan iki top aynı anda belirli bir yükseklikten bırakıldığında iki top farklı zamanlarda yere düşmeyecektir.

Yukarıdaki kısa diyaloglardan da anlaşılacağı üzere Galileo, Aristoteles’in cisimlerin hareketi ve hızı hakkındaki düşüncelerini kafasında çoktan çürütmüş ve yepyeni bir hareket yasalarının temellerini atmak üzeredir. Artık şu kesin bir olguydu: Ağır cisimler ile hafif cisimler aynı anda yere düşüyordu.

Ancak burada bir sorun var gibi gözüküyordu: Bazı hafif cisimleri gözlemleyenler, gerçekten de onların yere daha geç düştüğüne şahit oluyordu. Bunun sebebi ne olabilirdi?

Galileo bunun da cevabını vermişti. Son derece hafif bir cisim, örneğin bir kuş tüyü açısından hava direnci önemli bir etkendir. Çünkü hava molekülleri kuş tüyünün yere düşüşünü yavaşlatır ve gerçekten de geç düşmesini sağlar.

Ancak bu, ağır ve hafif cisimlerin yere aynı anda düştüğü gerçeğini değiştirmiyor. Sadece maddelerin yoğunluk farklılıkları, cisimlerin düşüş hızını etkileyebiliyor.

Galileo’nun Aristoteleşçi görüş aleyhine sunduğu bulgular ve yaklaşımı, “hareket bilimi” ya da “mekanik” alanının doğmasına zemin hazırlamıştı. Galileo, cisimlerin sürekli bir düşüş halinde olduğu gerçeğinden yola çıkarak, serbest düşüş hareketinin bütün cisimlere içkin bir hareket olduğunu fark etmişti.

Yani cisimler her zaman düşüyordu aslında. Bu bakış açısının önemini şu sözlerle vurguluyor Galileo:

Amacım, antik dönemden beri var olan meseleyle ilgili yeni bir bilim ortaya koymaktır. Doğada belki de hareketten daha temel bir olgu yoktur. Doğa filozoflarının bu konu hakkında yazdığı kitaplar az olmamakla birlikte ben de hareket konusuna ilişkin, şimdiye kadar gözlemlenmemiş ya da kanıtlanmamış olup, öğrenmeye değer bazı özellikler keşfettim. Ağır bir cismin yere düşüş hızının sürekli ivmelendiği şeklinde üstünkörü bazı deneyler yapılmıştır. Ancak deneyi yapanlar, bu ivmelenmenin ne dereceye kadar gerçekleştiğini belirtmemişler. Bu konu hakkında yaptığım çalışmalar ise hareket bilimi alanında sadece bir başlangıç niteliğindedir. Benden daha keskin zekalı diğer zihinler ise konunun daha da derinliklerine vakıf olmayı ileride başaracaklardır.

Galileo Galilei

Cisimlerin İvmeli Hareketi

Birçok insan cisimlerin düşüş sırasında aynı hızla düştüğü şeklinde yanlış bir algıya sahipti o dönemde. Böylece düşüşün hep aynı hızda gerçekleştiği sanılıyordu. Fakat Galileo bu durumun böyle olmadığına emindi ve cisimlerin düşüş hızı hakkında daha temel bir soruyu gündeme getirmişti: Düşüş sırasında cismin hızı ne ölçüde değişiyordu?

Ancak Galileo’nun bu soruyu cevaplayabilmesi için önünde bir engel bulunuyordu. Bir cismin sadece düşüşünü izleyerek onun ne kadar hızlandığını tespit edebilmek çok zordu. Bu, ancak yavaş çekimde mümkün olabilirdi.

Peki Galileo cismin düşüş hızını yavaş bir şekilde nasıl izleyebilirdi ki? Cevap: Cismin hızını azaltmak. Peki bu nasıl mümkün olacaktı?

Galileo, cismin doğrudan yere düşmesi yerine bir rampadan yuvarlanan top ile deney yapmayı öneriyordu. Böylece topun hız artış oranı değişmeden ne kadar hızlı bir şekilde ivmelendiğini ölçebilecekti.

Ayrıca rampanın eğimi de topun hız karakterini değiştirmeyecekti. Yani rampa eğimi ne olursa olsun top düzenli bir oranda ivmelenmeye devam edecekti.

Galileo şöyle düşünmüştü: Eğer top, daha dik bir rampaya bağlı olan az eğimli bir rampadan yuvarlanmaya bırakıldığı zaman, ilk rampada başladığı aynı yüksekliğe ikinci rampada da çıkacaktır.

Bir diğer ifadeyle ikinci rampanın eğimi ne olursa olsun topun iki rampadaki toplam hızı birbirine eşit olacağından ikinci rampada da aynı yüksekliğe erişecektir. Aşağıdaki görselde bu durumu daha net anlayabiliriz.

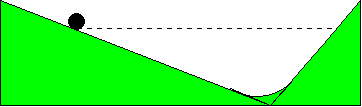
Galileo, iki rampadan da yuvarlanan topun hızının her iki durumda da birbirine eşit olduğunu anladıktan sonra, ikinci rampanın daha da dik olduğunu hayal etti. İkinci rampanın eğimi o kadar fazla olacaktı ki üzerindeki topun tıpkı yere düştüğü gibi bir hızda yuvarlanacağını düşündü.

Bu durumda yere dik düşen bir topun toplamda edindiği hızın, eğimli bir rampa üzerinde toplamda elde ettiği hıza eşit olduğu çıkarımını yapabiliriz. Aralarındaki tek fark ise dik düşen top, elde edeceği hıza daha kısa bir sürede ulaşıyordu. Böylece Galileo, cismin ivmelenme karakterini değiştirmeden cismin hızını yavaşlatmanın bir yolunu bulmuştu.

Zamanı Ölçmek

Galileo’nun, topun hızını ölçebilmesi için zaman tutması gerekiyordu. Çünkü topun ivmelenme karakteri, ancak topun ne kadar bir sürede düştüğü bilinerek belirlenebilirdi.

Fakat o dönemde cisimlerin düşüş hızını ölçüp süresini tutabilecek hassas aletlerin bulunmadığını söyleyebiliriz. İlk olarak Galileo, zamanı ölçebilmek için nabzını kullanmaya karar verdi. Lakin nabız, bu hususta çok da doğru bir zaman ölçümü vermiyordu. Sonrasında bir “su saati” kullanmanın, zamanı doğru bir şekilde ölçmesine yardım edebileceğini fark etti. Galileo bunun üzerine bir su saati tasarlamıştı.

Kaptaki suyun düzenli bir şekilde altındaki tasa damlamasından ibaret olan bu su saatinde Galileo, tastaki suyun ağırlığını tartarak ne kadar zamanın geçmiş olduğunu ölçebilecekti. Sıra artık deneyi yapmaya gelmişti.

Galileo’nun Eğik Düzlem Deneyi

Daha önce de söylendiği gibi Galileo, cisimlerin düşüş hızlarının zamana göre nasıl değiştiğini ölçmek istiyordu. Ancak havada bırakılan bir cismin yere düşmesi çok kısa bir zamanda gerçekleştiği için düşüş hızının hesaplanabilmesi bu açıdan çok zor bir işti.

Galileo tasarladığı zekice bir deneyle bu sorunun da üstesinden gelecekti: Eğik düzlem rampası. Galileo’nun bu mekanizması basitti. Ağaçtan yapılmış eğimli bir rampadan ve bir toptan oluşuyordu.

Top, eğimli rampanın en üstünden bırakıldığı zaman nispeten daha yavaş bir hızla aşağı doğru yuvarlanacaktı. Çünkü eğimli rampa, kütleçekimi kuvvetinin cisimleri ivmelendirme özelliğini azaltıyordu. Top yavaş bir şekilde yuvarlanacağından Galileo, hassas bir şekilde zaman ölçümünü gerçekleştirebilirdi artık.

Galileo Bulgularını Analiz Ediyor

Top, rampada yuvarlandıkça Galileo, onun düzenli bir şekilde artan bir hızla yuvarlandığını fark etti. Böylece topun yuvarlanması için geçen sürenin karesi ile topun aldığı mesafe arasında bir ilişkinin olduğu ortaya çıkmıştı. Bir diğer ifadeyle mesafe ile geçen zaman arasındaki oran lineer değildi.

Mesela topun bütün rampayı yuvarlanarak kat etmesi için altı saniye geçtiğini farz edelim. Şayet topun aynı uzunluğun yarısını kat etmesi için ne kadar zaman geçeceği şeklinde bir soru sorarsak, oran-orantı hesabından üç saniye olacağını söylerdik.

Ancak Galileo bunun böyle olmadığını keşfetmişti. Topun rampanın yarısını kat etmesi için üç yerine dört saniye geçiyordu. Rampanın tamamını kat etmesi için de altı saniye geçiyordu. Demek ki zaman geçtikçe alınan mesafe de ciddi bir biçimde artıyordu.

Yukarıdaki örneğe dikkat edilirse ilk üç saniyede top, rampanın yarısına kadar bile gelemeyecektir. Çünkü geçen zaman nispeten azdır. Ama 3.saniyeden sonra artık daha fazla zaman geçmiş olduğu için topun kat ettiği mesafe de zamanın karesi oranında artacak ve böylece ilk üç saniyeye göre daha fazla yol alacaktır.

Yani top 1.saniyede 1 birim uzunluk, 2.saniyede 4 birim uzunluk, 3.saniyede 9 birim uzunluk şeklinde, geçen zamanın karesiyle doğru orantılı bir mesafe kat edecektir.

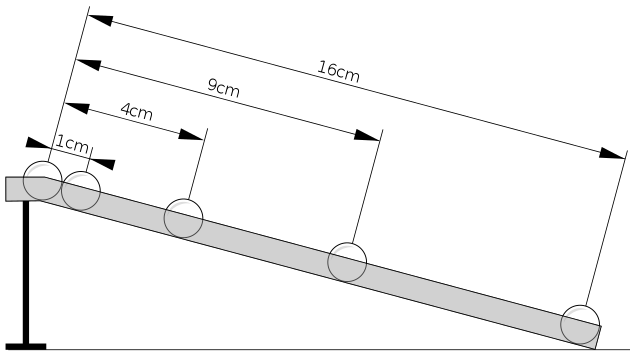
Deneyin Sonuçları ve Galileo’nun Mirası

Galileo’nun eğik düzlem deneyi, cisimlerin serbest düşüşte düzenli bir ivmelenmeye uğradığını gözlemsel olarak kanıtlıyordu. Eğik rampada yuvarlanan topun hızı sabit bir oranda artıyordu.

Bu düzenli ivmelenme olgusunun fark edilmesi, cismin süredurum(durağanlık) ilkesine de bir örnektir aynı zamanda. Şöyle ki bir cisme başlangıçta bir kuvvet uygulandığı zaman, başka bir kuvvet etki etmedikçe cisim, o ilk kuvvetin etkisi altında kalacaktır.

Galileo’nun farkına vardığı bu süredurum ilkesi, Isaac Newton’un hareket eden cisimler için formüle ettiği Hareket Kanunları’ndan olan Birinci Hareket Kanunu’nu geliştirmesinde çok büyük bir rol oynayacaktır.

Bu kanunlar, günümüzdeki mekanik ve fizik alanının temel yapı taşları niteliğindedir. Bu bağlamda Galileo’nun yaptığı çalışmalar ve deneylerin günümüzde bile ne kadar önemli bir rol oynadığını rahatlıkla görebiliriz.